6.1. TSUNAMI-1D: Control Module for One-Dimensional Cross-Section Sensitivity and Uncertainty
B. T. Rearden, M. A. Jessee, L. M. Petrie, and M. L. Williams
6.1.1. ABSTRACT
TSUNAMI-1D (Tools for Sensitivity and Uncertainty Analysis Methodology Implementation in One Dimension) is a SCALE control module that facilitates the application of sensitivity and uncertainty analysis theory to nuclear systems analyses. TSUNAMI-1D was originally developed to provide sensitivity and uncertainty analysis of keff for criticality safety applications, and subsequent updates provide for analysis of system responses other than keff, using generalized perturbation theory. TSUNAMI-1D provides for automated processing of material input, processing of cross-section data, calculation of neutron transport solutions, calculation of sensitivity coefficients, and the calculation of uncertainties in system responses due to cross-section-covariance data. The XSDRNPM module is used for the transport solver. XSDRNPM uses the method of discrete ordinates to calculate keff for applications that are appropriate for 1D modeling. The SAMS module is used to determine the sensitivities of the calculated value of keff and other system responses to the nuclear data used in the calculation as a function of nuclide, reaction type, and energy. The uncertainties in the calculated value of keff and other system responses, resulting from uncertainties in the basic nuclear data used in the calculation, are estimated using energy-dependent cross-section-covariance matrices. The implicit effects of the resonance self-shielding calculations are predicted using BONAMIST.
6.1.2. ACKNOWLEDGMENTS
The authors acknowledge Bryan Broadhead of Oak Ridge National Laboratory, and R. L. Childs, formerly of the Oak Ridge National Laboratory, for their assistance with this work. The support and encouragement of Calvin Hopper, Cecil Parks, and Don Mueller of Oak Ridge National Laboratory is also appreciated. Additionally, the authors wish to acknowledge Debbie Weaver and Sheila Walker for their assistance in preparing this document.
6.1.3. Introduction
TSUNAMI-1D (Tools for Sensitivity and Uncertainty Analysis Methodology Implementation in One Dimension) is a SCALE control module that facilitates the application of sensitivity and uncertainty theory to nuclear system analyses. The data computed with TSUNAMI-1D are the sensitivity of a system response, such as keff, to each constituent cross-section data component used in the calculation. The sensitivity data are coupled with cross-section uncertainty data, in the form of multigroup covariance matrices, to produce an uncertainty in the system response due to uncertainties in the underlying nuclear data. The group-wise sensitivity data computed with TSUNAMI-1D are stored in a sensitivity data file (.sdf file) that is suitable for use in assessing system similarity for code validation purposes using TSUNAMI-IP, (see TSUNAMI-IP chapter), and for advanced bias assessment using TSURFER, see the TSURFER chapter.
This manual is intended to provide the user with a detailed reference on code input options and provide some examples of the application of TSUNAMI-1D to generate sensitivity and uncertainty data. A detailed description of code input is provided in Sect. 6.1.4, three sample problems are given in Sect. 6.1.5 the techniques used in each computational sequence are described in Sect. 6.1.3.1, and additional information is provided in the appendices. A new user may wish to begin by reviewing the sample problems, and then refer to the input details in Sect. 6.1.4 to customize an input for his specific needs.
TSUNAMI-1D provides automated, problem-dependent cross sections using the same methods and input as the Criticality Safety Analysis Sequences (CSAS). The BONAMIST code computes the sensitivity of resonance self-shielded cross to the input data, the so-called “implicit sensitivities.”
After the cross sections are processed, the TSUNAMI-1D sequence performs two XSDRNPM criticality calculations, one forward and one adjoint. Finally, the sequence calls the SAMS module to calculate the sensitivity coefficients that indicate the sensitivity of the calculated values to changes in the cross sections and the uncertainty in the calculated value due to uncertainties in the basic nuclear data. SAMS prints energy-integrated sensitivity coefficients and their statistical uncertainties to the SCALE output file and generates a separate data file containing the energy-dependent sensitivity coefficients.
In addition to the sensitivity and uncertainty analysis sequence, the TSUNAMI-1DC sequence can be used to verify the accuracy of the TSUNAMI-1D calculations with direct perturbation criticality calculations. The verification of computed sensitivity coefficients is imported for systems where the cell-weighted material is not the only material used in the model. By default, TSUNAMI-1DC performs the same functions as the TSUNAMI-1D sequence with PARM=CENTRM, except that it does not perform the adjoint XSDRNPM calculation and does not call the SAMS module.
6.1.3.1. TSUNAMI-1D Techniques
TSUNAMI-1D is a SCALE control module. As such, its primary function is to control a sequence of calculations that are performed by other codes. The input for each of the TSUNAMI-1D sequences is very similar to that used for CSAS1, with the addition of the system model description and optional sensitivity calculation data. TSUNAMI-1D uses the same material and cell data input as all other SCALE sequences. The control sequences available in TSUNAMI-1D are summarized in Table 6.1.1, where the functional modules executed by each control sequence are also shown. A general flow diagram of TSUNAMI-1D is shown in Fig. 6.1.1.
Control module |
Functional modules executed by the control module |
||||
|---|---|---|---|---|---|
TSUNAMI-1D |
XSProc |
XSDRNPM forward |
XSDRNPM adjoint* |
BONAMIST |
SAMS* |
TSUNAMI-1DC |
XSProc |
XSDRNPM forward |
|||
* The XSDRNPM adjoint calculation and SAMS calculation on are repeated for each system response defined by the user. |
|||||
TSUNAMI-1D and many other SCALE sequences apply a standardized procedure to provide appropriate cross sections for the calculation. This procedure is carried out by routines of the XSProc that generate number densities and related information, prepare geometry data for resonance self-shielding and flux-weighting cell calculations, and create data input files for the cross-section processing codes.
By default, the TSUNAMI-1D sequence performs cross-section processing with XSProc, exercising all available options there, performs the forward and adjoint XSDRNPM calculations, calls BONAMIST to produce implicit sensitivity coefficients, then calls SAMS to produce sensitivity and uncertainty output and sdf files. Optional sequence level parameters can be used to change methods applied in resonance self-shielding and exclude the implicit sensitivity calculation, which detailed later in this document. If additional system responses are requested in the input, TSUNAMI-1D executes additional generalized adjoint XSDRNPM and SAMS calculations for each system response.
The input requirements for the model description are very similar to
those used for multiregion cell descriptions in the cell data section of
input. The definition of system responses other than keff requires
both the DEFINITIONS and SYSTEMRESPONSE block of input data. These
blocks of data are described in Sect. 6.1.4.4. TSUNAMI-1D also reads
and prepares inputs for the SAMS calculation. The additional input
blocks for the SAMS module are optional. The input format of the SAMS
blocks of data are described in the SAMS chapter.

Fig. 6.1.1 General flow diagram of TSUNAMI-1D.
6.1.4. TSUNAMI-1D Input Description
The input to TSUNAMI-1D consists of a SCALE Analytical Sequence
Specification Record, SCALE XSProc data, model problem data, optional
sensitivity and uncertainty calculation data, and optional system
response characterization data. The data for each of these segments are
entered using the SCALE free-form format, allowing alphanumeric data,
floating-point data, and integer data to be entered in an unstructured
manner. The input is not case sensitive, so either upper- or lowercase
letters may be used. A maximum of 252 columns per line may be used for
input. Data can usually start or end in any column with a few
exceptions. As an example, the word END beginning in column 1 and
followed by two blank spaces will end the problem, any data following
will be ignored. Each data entry must be followed by one or more blanks
to terminate the data entry. For numeric data, either a comma or a blank
can be used to terminate each data entry. Integers may be entered for
floating values. For example, 10 will be interpreted as 10.0. Imbedded
blanks are not allowed within a data entry unless an E precedes a single
blank as in an unsigned exponent in a floating-point number. For
example, 1.0E 4 would be correctly interpreted as 1.0 \(\times\) 104. A
comment is initiated with a single quote, '', and continues until the end
of the input line.
6.1.4.1. Analytical sequence specification record
The analytical sequence specification begins in column 1 of the first line of the input file and must contain one of the following:
- =TSUNAMI-1D
This sequence is used for sensitivity and uncertainty calculations.
- =TSUNAMI-1DC
This sequence allows more flexibility than CSAS1 and is used for criticality calculations where the criticality problem description contains more detail than that specified in a single unit cell description.
Optional keyword input may be entered, starting after column 10 of the analytical sequence specification record. These keywords are
- PARM=CHECK
This option allows the input data to be read and checked without executing any functional modules.
- PARM=CHK
Alias for
PARM=CHECK.
- PARM=SIZE=n
The amount of memory requested in four-byte words may be set with this entry. The default value for n is 20000000. This value only affects calculations in BONAMIST, where this value of the
SIZEparameter is used for allocation of storage for the derivatives. Please see the documentation on BONAMIST in the Sensitivity Utility Modules chapter for more details. All other codes use dynamic memory allocation and this value has no effect.
- PARM=BONAMIST
This is the default configuration for MG TSUNAMI-1D calculations. XSProc with BONAMI and CENTRM is used for cross-section processing, and implicit sensitivities are produced with BONAMIST.
- PARM=CENTRM
XSProc with BONAMI and CENTRM is used for cross-section processing, but BONAMIST is not run. TSUNAMI-1D sequence with
PARM=CENTRMdoes not produce the implicit portions of the sensitivity coefficients, and should be used with caution.
- PARM=BONAMI
XSProc with BONAMI is used for cross-section processing, but BONAMIST is not run. TSUNAMI-1D sequence with
PARM=BONAMIdoes not produce the implicit portions of the sensitivity coefficients, and should be used with caution.
- PARM=2REGION
XSProc with BONAMI and CENTRM are run where Dancoff factors are to compute the escape probabilities for an accelerated, yet more approximate, CENTRM calculation. Implicit sensitivities are computed with BONAMIST.
Multiple parameters can be used simultaneously by enclosing them in parentheses and separating them with commas such as PARM=(SIZE=2000000, CHECK).
Multiple parameters can be used simultaneously by enclosing them in parentheses and separating them with commas such as PARM=(SIZE=2000000, CHECK).
6.1.4.2. XSProc
XSProc reads the standard composition specification data and the unit cell geometry specifications. It then produces the mixing table and unit cell information necessary for processing the cross sections. The XSProc chapter provides a detailed description of the input data for the Material Information Processor.
6.1.4.3. Model problem data
The model problem data are used by the TSUNAMI-1D sequences to prepare input for the XSDRNPM transport calculation. This input section consists of two data blocks, one block contains a geometry description and one contains optional parameters.
6.1.4.3.1. Geometry data
The TSUNAMI-1D geometry data block begins with the keywords READ GEOM
and ends with the keywords END GEOM. This data block is always
required. The following data is contained within this data block:
A line containing the geometry and boundary conditions for the XSDRNPM criticality case. The first entry on this line describes the geometry and must be SLAB, CYLINDRICAL, or SPHERICAL. The second entry is optional and describes the right-boundary condition. The default value for the right-boundary condition is VACUUM. The third entry on this line is optional and describes the left-boundary condition. The default value for the left boundary condition is REFLECTED. The last entry on this line is END. Valid entries for the boundary conditions are the following:
VACUUM – No return at boundary
REFLECTED – Specular (mirror-like) return at boundary
PERIODIC – Infinite array of cells in slab geometry
WHITE – Isotropic return at boundary
A line containing the following two entries for each zone of the XSDRNPM case:
mixture number in the zone and
zone outer dimension (in cm).
Mixture numbers and zone dimensions are entered in pairs until the entire geometry is defined. The mixture numbers must be defined in the material input processor input. Mixture 0 is used for voids, and a mixture number defined with CELLMIX= in the MIP section of the input may be used here. It should be noted that, due to a restriction in XSDRNPM, the mixture number identified with CELLMIX= may not appear in the output file, even though it is input in this section. TSUNAMI-1D automatically renumbers the cell mixed mixture to the next available mixture number for use in XSDRNPM. A message is printed in the output identifying this change. TSUNAMI-1D uses the same techniques as CSAS1X to automatically prepare a spatial mesh appropriate for the input materials and dimensions.
6.1.4.3.2. Parameter data
An optional data block may be entered to change parameters of the
XSDRNPM forward and adjoint calculations. This data block begins with
the keywords READ PARA or READ PARM and must end with either
END PARA or END PARM, corresponding to the read keyword. In this
data block, the user may enter optional lines that contain entries for
selected XSDRNPM input parameters. A list of the parameters and their
default values are found in Table 6.1.2.
Name |
Default |
Meaning |
|---|---|---|
|
16 |
Order of angular quadrature |
|
20 |
Inner-iteration maximum |
|
100 |
Outer-iteration maximum |
|
-1 |
Flux-edit option: |
-1 no flux print |
||
0 scalar flux print |
||
1 scalar and angular flux print |
||
|
5 |
Order of Legendre expansion for cross sections |
|
-2 |
Cross-section print option: |
-2 no cross-section print |
||
-1 print 1-D cross sections |
||
0/N print 2-D cross sections through order N |
||
|
0 |
Balance table print option: |
-1 no balance table print |
||
0 fine group balance table print |
||
|
1.E-6 |
Outer-iteration convergence criteria |
|
1.E-6 |
Inner-iteration convergence criteria |
|
0 |
First-transverse dimension (cm) for buckling correction (i.e., height of cylinder or slab) |
|
0 |
Second-transverse dimension (cm) for buckling correction (i.e., depth of slab) |
|
1.5 |
Size factor of spatial computational mesh intervals. Increasing this number will cause the forward and adjoint XSDRNPM calculations to be conducted with larger mesh intervals and fewer mesh points. 0.0<SZF<1.5 gives a finer mesh, SZF>1.5 gives a coarser mesh. |
6.1.4.4. Sensitivity and uncertainty calculation data
The data blocks for controlling the sensitivity and uncertainty
calculation are optional. The optional data blocks include the SAMS
block, the HTML block, the COVARIANCE block, the DEFINITIONS
block, and the SYSTEMRESPONSES block. These data blocks begin with the
keywords READ BLOCKNAME and end with the keywords END BLOCKNAME,
where BLOCKNAME is one of SAMS, HTML, COVARIANCE,
DEFINITONS, or SYSTEMRESPONSES. These data blocks can be input in any
order with the following two exceptions. First, all five data blocks must
appear in the input file after the composition and cell data blocks of data.
Second, if a SAMS block is specified, the HTML and COVARIANCE data
blocks must come after the SAMS block, if they are to be specified. In
addition, both the DEFINITONS and SYSTEMRESPONSES data blocks must
be present for additional analysis of system responses other than
keff. If only one or both of the data blocks are omitted, then
analysis is only performed for keff. The following sub-sections
describe these blocks of data in detail.
6.1.4.4.1. Response definition data
The DEFINITIONS and SYSTEMRESPONSES blocks are used to define system
responses for additional sensitivities and uncertainty analysis in SAMS.
For criticality calculations, the sensitivities of system responses
other than keff are calculated in TSUNAMI-1D using generalized
perturbation theory (GPT). The details of the GPT methodology are
provided in General Perturbation Theory section of the SAMS chapter.
Using GPT, a system response, denoted R, is defined as a ratio such
as:
In this equation, \(\phi_{g}(\bar{r})\) is the space-dependent multi-group scalar
flux and \(H_{N, g}(\bar{r})\),\(H_{D, g}(\bar{r})\) are referred to as the space-dependent,
multi-group response functions. In TSUNAMI-1D, the response functions
are specified in the DEFINITIONS data block and the system
responses are defined in the SYSTEMRESPONSES data block. Responses
(other keff) treated in TSUNAMI-1D MUST be ratios.
The DEFINITIONS data block is used by TSUNAMI-1D similarly to that of
the MAVRIC and MONACO modules in SCALE. The format of the DEFINITIONS
block is as follows:
read definitions
response I1
(specifications for response I1)
end response
response I2
(specifications for response I2)
end response
...
end definitions
The DEFINITIONS block of data begins with READ DEFINITIONS and
terminates with END DEFINITIONS. Likewise, each response function
definition begins with RESPONSE - followed by a unique, positive
integer identifier - and terminates with END RESPONSE. The keyword
entries summarized in Table 6.1.3 are allowed for each response
specification. Keywords ending with = must be followed by the value to
be assigned to the corresponding variable. All keywords are optional and
can be entered in any order. However certain keywords are required
depending one of the seven basic types of response functions described
in the following subsections. The required keywords are summarized for
each of the seven basic response function types in Table 6.1.3 at the
end of this section.
Keyword |
Type |
Default value |
Description |
|---|---|---|---|
|
String |
” “ |
Response function title. The title must begin and end with quotes and have a maximum of 256 characters. |
|
Logical |
F |
Macroscopic cross-section flag. If specified, macroscopic cross-sections are used to define the response function. |
|
Logical |
T |
Microscopic cross-section flag. If specified, microscopic cross-sections are used to define the response function. |
or
|
Integer or string |
Undefined |
Nuclide identifier for which cross-sections are used to define the response function. The nuclide can be specified in integer format (92235) or in character string format (u-235). |
or
|
Integer or string |
Undefined |
Reaction identifier for which cross-sections are used to define the response function. The reaction can be specified as an MT number (18) or as a character string (fission). Supported reaction types are listed below. |
or
|
Integer |
Undefined |
Mixture identifier for which cross-sections are used to define the response function. |
|
Integer array |
Undefined |
Array of mixture identifiers for which cross-sections cross-sections are used to define the response function. |
|
Logical |
F |
Flux response function flag. If specified, cross-sections are not used to define the response function. |
|
Real |
1.0 |
Response function multiplier. |
|
Real |
1025 |
Upper energy (eV) boundary of the response function. |
|
Real |
0.0 |
Lower energy (eV) boundary of the response function. |
|
Real |
1025 |
Upper energy (eV) boundary used for cross-sections with secondary particle distributions (elastic, inelastic, scatter, and n,2n). |
|
Real |
0.0 |
Lower energy (eV) boundary used for cross-sections with secondary particle distributions (elastic, inelastic, scatter, and n,2n). |
6.1.4.4.1.1. Single-mixture flux response function
A single-mixture flux response is simply the integration of the neutron flux wherever a specified mixture is defined in the problem geometry. Therefore, the response function \(H_{g}(\bar{r})\) for a single mixture-j is defined as:
where
In this expression, the constant c is the scalar multiplier defined by
the multiplier= keyword. For example, the “fast” and “thermal” flux
responses for mixture 5 would be:
In this example, the energy cutoff between the fast group and the
thermal group is defined as 0.625 eV. Response 3 reflects the total
energy-integrated flux-scaled by a factor of 2.0-because the default
values of eHigh and eLow are used.
For single-mixture flux responses, keywords unity and mixture are
required; multiplier, eHigh, and eLow are optional; title,
nuclide, reaction, micro, macro, eHighTransfer, and
eLowTransfer are optional but are not used; and multimix is not
allowed. These keyword dependencies are outlined for each response type in
Table 6.1.4.
6.1.4.4.1.2. Multiple-mixture flux response
A multiple-mixture flux response is the integration of the neutron flux wherever a set of mixtures are defined in the problem geometry. Therefore, the response function \(H_{g}(\bar{r})\) for a set of mixtures “S” is defined as:
For example, the following definition is for the energy-integrated flux response, and spatially-integrated wherever mixtures 5, 7, and 9 are used:
read definitions
response 1 unity multimix 5 7 9 end end response
end definitions
or alternatively,
read definitions
response 1 multimat 5 7 9 end unity end response
end definitions
For multiple-mixture flux responses, keywords unity and multimix are
required; multiplier, eHigh, and eLow are optional; title,
nuclide, reaction, micro, macro, eHighTransfer, and
eLowTransfer are optional but are not used; and mixture is not allowed.
6.1.4.4.1.3. Single-mixture, single-nuclide, microscopic cross-section response
A single-mixture, single-nuclide, microscopic cross-section response is the integration of the neutron flux multiplied by a microscopic cross-section. The microscopic cross-section used in the integral is defined by a specific mixture, nuclide, and reaction type. Therefore, the response function \(H_{g}(\bar{r})\) is defined as:
In this expression, \(\sigma_{x, g}^{j, n}\) is the microscopic cross-section for mixture-j, nuclide-n, reaction type-x, and energy group-g. For transfer reaction types-scatter, elastic, inelastic, and n,2n-the expression above is slightly modified so the user can define the energy range of the secondary particles, i.e.,
where
Likewise, the expression for \(H_{g}(\bar{r})\) is also modified for fission distribution responses (chi), which are usually integrated by the energy-integrated neutron production rate rather than the neutron flux:
For examples of this response type, the following DEFINITION block has
response definitions for
total nu-fission rate of U-235 in mixture 1,
“fast” n,gamma capture rate of U-238 in mixture 1 (energy cutoff is 0.625 eV),
downscatter rate of H-1 in mixture 2, and
number fission neutrons born from Pu-239 fissions in mixture 1 in the intermediate energy range (E>0.625 eV and E<25 keV)
read definitions
response 1
reaction=nu-fission mixture=1 nuclide=92235
end response
response 2
reaction=n,gamma mixture=1 nuclide=u-238 eLow=0.625
end response
response 3
mt=0 mixture=2 zaid=1001 eLow=0.625 eHighTransfer=0.635
end response
response 4
mt=chi mixture=1 zaid=pu-239 eHigh=25.0e3 eLow=0.625
end response
end definitions
For single-mixture, single-nuclide microscopic cross-section responses,
keywords mixture, nuclide, and reaction are required;
multiplier, eHigh, eLow, eHighTransfer, eLowTransfer, and
micro, are optional; title is optional but not used; and multimix,
macro, and unity are not allowed. A list of supported cross-section
reaction types is provided at the end of this section in Table 6.1.5.
6.1.4.4.1.4. Single-mixture, single-nuclide, macroscopic cross-section response
A single-mixture, single-nuclide, macroscopic cross-section response is the integration of the neutron flux multiplied by a macroscopic cross-section. The macroscopic cross-section used in the integral is defined by a specific mixture, nuclide, and reaction type. The response function \(H_{g}(\bar{r})\) is defined as:
In this expression, \(\Sigma_{x, g}^{j, n}\) is the macroscopic cross-section (\(N^{j,n} * \sigma^{j,n}_{x,g}\)) for mixture-j, nuclide-n, reaction type-x, and energy group-g. The modifications to this expression for transfer reactions and chi are similar to that of single-mixture, single-nuclide, microscopic cross-section responses. Using the same example as above, the single-mixture, single-nuclide, macroscopic cross-section responses are given as:
read definitions
response 1
reaction=nu-fission mixture=1 nuclide=92235 macro
end response
response 2
reaction=n,gamma mixture=1 nuclide=u-238 eLow=0.625 macro
end response
response 3
mt=0 mixture=2 zaid=1001 eLow=0.625 eHighTransfer=0.635 macro
end response
response 4
mt=chi mixture=1 zaid=pu-239 eHigh=25.0e3 eLow=0.625 macro
end response
end definitions
For single-mixture, single-nuclide macroscopic cross-section responses,
keywords mixture, nuclide, macro, and reaction are required;
multiplier, eHigh, eLow, eHighTransfer, and eLowTransfer,
are optional; title is optional but not used; and multimix, micro,
and unity are not allowed.
6.1.4.4.1.5. Single-mixture, multiple-nuclide, macroscopic cross-section response
A single-mixture, multiple-nuclide, macroscopic cross-section response is the integration of the neutron flux multiplied by a macroscopic cross-section. The macroscopic cross-section used in the integral is defined by a specific mixture, and reaction type. The response function \(H_{g}(\bar{r})\) is defined as:
In this expression, \(\Sigma_{x, g}^{j}\) is the mixture macroscopic cross-section defined as \(\sum_{n}N^{j,n} * \sigma^{j,n}_{x,g}\) for mixture-j, reaction type-x, and energy group-g. The modifications to this expression for transfer reactions is similar to that defined in previous subsections. For mixture chi responses, \(H_{g}(\bar{r})\) is rewritten as
For examples of this response type, the following DEFINITIONS block
has response definitions for
total nu-fission rate in mixture 1,
“fast” n,gamma capture rate in mixture 1 (energy cutoff is 0.625 eV),
downscatter rate in mixture 2, and
number fission neutrons born in mixture 1 in the intermediate energy range (E>0.625 eV and E<25 keV)
read definitions
response 1
reaction=nu-fission mixture=1 macro
end response
response 2
reaction=n,gamma mixture=1 eLow=0.625 macro
end response
response 3
mt=0 mixture=2 eLow=0.625 eHighTransfer=0.635 macro
end response
response 4
mt=chi mixture=1 eHigh=25.0e3 eLow=0.625 macro
end response
end definitions
For single-mixture, multiple-nuclide macroscopic cross-section
responses, keywords mixture, macro, and reaction are required;
multiplier, eHigh, eLow, eHighTransfer, and eLowTransfer,
are optional; title is optional but not used; and multimix, micro,
nuclide, and unity are not allowed.
6.1.4.4.1.6. Multiple-mixture, single-nuclide, macroscopic cross-section response
A multiple-mixture, single-nuclide, macroscopic cross-section response is the integration of the neutron flux multiplied by a macroscopic cross-section over a set of mixtures defined in the problem geometry. The macroscopic cross-section used in the integral is defined by a specific mixture, nuclide, and reaction type. The response function \(H_{g}(\bar{r})\) is defined as:
In this expression, \(\Sigma_{x, g}^{j, n}\) is the macroscopic cross-section (\(N^{j,n} * \sigma^{j,n}_{x,g}\)) for mixture-j, nuclide-n, reaction type-x, and energy group-g. The summation of mixtures in this expression is for a set of user-defined mixtures, denoted S. The modifications to this expression for transfer reactions and chi are applied similarly to previously defined response types above.
For examples of this response type, the following DEFINITIONS block
has response definitions for
total nu-fission rate of U-235 in the fuel mixtures (mixtures 1,3,5)
“fast” n,gamma capture rate of U-238 in the fuel mixtures
downscatter rate of H-1 in the moderator mixtures (mixtures 2,4)
number fission neutrons born in the intermediate energy range (E>0.625 eV and E<25 keV) in Pu-239 in the fuel mixtures
read definitions
response 1
reaction=nu-fission multimix 1 3 5 end macro zaid=92235
end response
response 2
reaction=n,gamma multimix 1 3 5 eLow=0.625 macro zaid=u-238
end response
response 3
mt=0 multimix 2 4 end eLow=0.625 eHighTransfer=0.635 macro zaid=h-1
end response
response 4
mt=chi multimix 1 3 5 end eHigh=25.0e3 eLow=0.625 macro zaid=pu-239
end response
end definitions
For multiple-mixture, single-nuclide macroscopic cross-section
responses, keywords multimix, nuclide, macro, and reaction are
required; multiplier, eHigh, eLow, eHighTransfer, and
eLowTransfer, are optional; title is optional but not used; and
mixture, micro, and unity are not allowed.
6.1.4.4.1.7. Multiple-mixture, multiple-nuclide, macroscopic cross-section response
A multiple-mixture, multiple-nuclide, macroscopic cross-section response is the integration of the neutron flux multiplied by a macroscopic cross-section over a set of mixtures defined in the problem geometry. The macroscopic cross-section used in the integral is defined by a specific mixture, and reaction type. The response function \(H_{g}(\bar{r})\) is defined as:
In this expression, \(\Sigma_{x, g}^{j}\) is the mixture macroscopic cross-section for mixture-j and reaction type-x, and energy group-g. The summation of mixtures in this expression is for a set of user-defined mixtures, denoted S. The modifications to this expression for transfer reactions and chi are applied similarly to the previously defined response types above.
For examples of this response type, the following DEFINITIONS block
has response definitions for
total nu-fission rate in the fuel mixtures (mixtures 1,3,5)
“fast” n,gamma capture rate in the fuel mixtures
downscatter rate in the moderator mixtures (mixtures 2,4)
number fission neutrons born in the intermediate energy range (E>0.625 eV and E<25 keV) in the fuel mixtures
read definitions
response 1
reaction=nu-fission multimix 1 3 5 end macro
end response
response 2
reaction=n,gamma multimix 1 3 5 eLow=0.625 macro
end response
response 3
mt=0 multimix 2 4 end eLow=0.625 eHighTransfer=0.635 macro
end response
response 4
mt=chi multimix 1 3 5 end eHigh=25.0e3 eLow=0.625 macro
end response
end definitions
For multiple-mixture, multiple-nuclide macroscopic cross-section
responses, keywords multimix, macro, and reaction are required;
multiplier, eHigh, eLow`, ``eHighTransfer, and eLowTransfer,
are optional; title is optional but not used; and mixture, micro,
nuclide, and unity are not allowed.
Response type |
Required keywords |
Unallowed keywords |
Optional keywords |
Optional, but not used keywords |
|---|---|---|---|---|
Single-mixture flux |
unity, mixture |
multimix |
multiplier, eHigh, eLow |
title, nuclide, reaction, micro, macro, eHighTransfer, eLowTransfer |
Multiple-mixture flux |
unity, multimix |
mixture |
multiplier, eHigh, eLow |
title, nuclide, reaction, micro, macro, eHighTransfer, eLowTransfer |
Single-mixture, single-nuclide, microscopic cross-section |
mixture, nuclide, reaction |
unity, macro, multimix |
multiplier, eHigh, eLow, micro, eHighTransfera , eLowTransfera |
title |
Single-mixture, single-nuclide, macroscopic cross-section |
mixture, nuclide, reaction,macro |
unity, micro, multimix |
multiplier, eHigh, eLow, eHighTransfera , eLowTransfera |
title |
Single-mixture, multiple-nuclide, macroscopiccross-section |
mixture, reaction,macro |
unity, micro, multimix, nuclide |
multiplier, eHigh, eLow, eHighTransfera , eLowTransfera |
title |
Multiple-mixture, single-nuclide, macroscopic cross-section |
multimix, nuclide reaction,macro |
unity, micro, mixture |
multiplier, eHigh, eLow, eHighTransfera , eLowTransfera |
title |
Multiple-mixture, multiple-nuclide, macroscopic cross-section |
multimix, reaction,macro |
unity, micro, mixture, nuclide |
multiplier, eHigh, eLow, eHighTransfera , eLowTransfera |
title |
aKeywords scatter (mt=0), elastic (mt=2), inelastic (mt=4), and n,2n (mt=16) For all other reaction types, these keywords are optional, but not used |
||||
MT |
Reaction |
String Identifier |
|---|---|---|
1 |
total |
Total |
2 |
elastic scattering |
Elastic |
4 |
inelastic scattering |
Inelastic |
16a |
effective n,2n |
n,2n |
0 |
sum of scattering (2+4+16) |
Scatter |
18 |
fission |
Fission |
102 |
n, \(gamma\) |
n,gamma |
103 |
n,p |
n,p |
104 |
n,d |
n,d |
105 |
n,t |
n,t |
106 |
n,3he |
n,he-3 |
107 |
n, \(alpha\) |
n,alpha |
101 |
Neutron disappearance (102+103+104+105+106+ 107) |
capture |
452 |
\(\bar{\nu}\) |
nubar |
1452 |
\(\bar{\nu}\) times fission |
nu-fission |
1018 |
\(\chi\) |
chi |
aThe effective n,2n is defined by the summation of transfer matrices of the following reaction types: (n,2n), (n,2n+\(\alpha\)), (n,2n+2\(\alpha\)), (n,3n), (n,3n+\(\alpha\)), and (n,4n). The individual transfer matrices are scaled by the number of exit channel neutrons, i.e., 2, 3, or 4. |
||
6.1.4.4.2. System response definition data
The SYSTEMRESPONSES block is used to define the set of system
responses for which TSUNAMI-1D will perform sensitivity and uncertainty
analysis additional to keff. For SCALE 6.1, only system response
ratios are supported in TSUNAMI-1D. The system response ratios are
defined from the response function definitions created in the
DEFINITIONS block. The format of the SYSTEMRESPONSES block is as
follows:
read systemresponses
ratio I1
(specifications for response ratio I1)
end ratio
ratio I2
(specifications for response ratio I2)
end ratio
...
end systemresponses
The SYSTEMRESPONSES block of data begins with READ SYSTEMRESPONSES
and terminates with END SYSTEMRESPONSES. Likewise, each system
response ratio definition begins with RATIO - followed by a unique,
positive integer identifier - and terminates with END RATIO. For each
response ratio definition, the keywords title=, numer, and denom
are allowed in any order. The title= specification is optional.
However, if specified, the title must be begin and end with quotes and
have a maximum of 20 characters. If omitted, the title of the ratio is
“rsp ratio NNNNNNNNNN” where NNNNNNNNNN is a zero-padded 10-digit
integer that is equal to the ratio identifier. The title is used as
labels in both the TSUNAMI-1D text and html output. The title is also
used by SAMS to generate the filename for the sensitivity data file for
the ratio system response discussed further below.
The numer array is a list of integers that correlate to response
function identifiers defined in the DEFINITIONS block. These response
functions are added together to form the composite response function
used in the numerator of the ratio. Likewise, the denom array is a
list of integers that correlate to response function identifiers defined
in the DEFINITIONS block. These response functions are added together
to form the composite response function used in the denominator of the
response ratio. Multiple response function ratios can be defined in a
single input file.
For a simple example of the SYSTEMRESPONSES block, suppose the ratio
system response of interest is the resonance escape probability for a
given system. Using 2-group theory, this is equivalent to the following
expression:
where \(\Sigma_{r, g}(\bar{r})\) is the removal cross-section defined as the total cross-section minus the within group cross-section — \(\Sigma_{t, g}(\bar{r})-\Sigma_{s, g \rightarrow g}(\bar{r})\). The TSUNAMI-1D model uses three mixtures whose ids are 6, 7, and 10. The thermal energy cutoff is 0.625 eV.
This ratio can be defined in multiple ways. First, the ratio can be defined with three response function definitions:
read definitions
response 1 title="DownScatter"
reaction=scatter
multimix 6 7 10 end
macro
eLow=0.625 eHighTransfer=0.625
end response
response 2 title="Fast Total"
reaction=total
multimix 6 7 10 end
macro
eLow=0.625
end response
response 3 title="Fast Within Group (times -1)"
reaction=scatter
multimix 6 7 10 end
macro
eLow=0.625 eLowTransfer=0.625
factor=-1.0
end response
end definitions
read systemresponses
ratio 100
title="Res Escape"
numer 1 end
denom 2 3 end
end ratio
end systemresponses
In the above input, the numerator of the response ratio is defined by a
single response function (id=1), which represents the rate at which
neutrons slow down from fast energies to slow energies. The denominator
of the response ratio is defined by two response functions (id=2 and
id=3). The addition of these two response functions represents the
“total minus within group scattering” calculation to formulate the fast
neutron removal rate. In this input, the title of the response ratio is
set to “Res Escape”. Because only one response ratio is defined, TRITON
will invoke SAMS twice, first for the keff sensitivity and
uncertainty analysis and second for the analysis of the resonance escape
probability. SAMS will generate two .sdf files, the first will be
jobname.sdf for keff sensitivities and the second will be
jobname.Res_Escape.sdf. jobname is the name of the input file. An
underscore is used to replace blanks and special characters in the
response ratio title in the sdf filename.
Similarly, the resonance escape probability can be defined in a variety of different ways. For example, the numerator response function can be expressed as the sum of individual mixture downscattering rates:
read definitions
response 2 title="Fast Total"
reaction=total
multimix 6 7 10 end
macro
eLow=0.625
end response
response 3 title="Fast Within Group (times -1)"
reaction=scatter
multimix 6 7 10 end
macro
eLow=0.625 eLowTransfer=0.625
factor=-1.0
end response
response 6 mt=0 mixture= 6 macro eLow=0.625 eHighTransfer=0.625
end response
response 7 mt=0 mixture= 7 macro eLow=0.625 eHighTransfer=0.625
end response
response 10 mt=0 mixture=10 macro eLow=0.625 eHighTransfer=0.625
end response
end definitions
read systemresponses
ratio 100
numer 6 7 10 end
denom 2 3 end
end ratio
end systemresponses
In this input, the numerator of the response ratio is defined by adding
the individual mixture downscattering rates together. Because a title
was not given for the response ratio, SAMS will generate the filename of
the response ratio sdf file as jobname.rsp_ratio_0000000100.sdf.
6.1.4.4.3. SAMS data
The SAMS block is used for controlling certain aspects of the
sensitivity and uncertainty calculation. This data block begins with the
keywords READ SAMS and ends with the keywords END SAMS. Any of the
optional SAMS input data may be entered in free form format between the
READ SAMS and END SAMS keywords. This optional SAMS input data is
shown in:
Table 6.1.6, with the default values specific to TSUNAMI-1D. Parameters
used to specify default covariance data to supplement or correct values
on the files specified by coverx= are shown in Table 6.1.7. A more
detailed explanation of the SAMS parameters may be found in the SAMS
chapter.
Keyword |
Default value |
Description |
binsen |
F |
Produces SENPRO formatted binary sensitivity data file on unit 40 |
coverx= |
56groupcov7.1 |
Name of covariance data file to use for uncertainty analysis |
largeimp= |
100.0 |
Value for the absolute value of implicit sensitivities, which if exceeded, will be reset to 0.0 and print a warning message. |
nocovar |
T |
Flag to cause uncertainty edit to be turned off (sets print_covar to F) |
nohtml |
F |
Flag to cause HTML output to not be produced. |
nomix |
F |
Flag to cause the sensitivities by mixture to be turned off |
pn= |
3 |
Legendre order for moment calculations |
prtgeom |
F |
Flag to cause the sensitivities to be output for each geometry region |
prtimp |
F |
Prints explicit sensitivities coefficients, implicit sensitivity coefficients and complete sensitivity coefficients |
prtvols |
F |
Flag to cause the volumes of the regions to be printed by SAMS |
unconstrainedchi |
F |
Flag to generate pre-SCALE 6 unconstrained chi (fission spectrum) sensitivities |
Keyword |
Default value |
Description |
use_dcov |
F |
Use default covariance data |
use_icov |
F |
Use user-input covariance data |
cov_fix |
F |
Correct covariance data if the uncertainty is large >1000% or zero |
large_cov |
10.0 |
Relative Standard
deviation to apply
|
return_work_cov |
F |
Create a new covariance data file with only the cross-section covariance data used in the analysis. |
udcov= |
0.05 |
User-defined default value of standard deviation in cross-section data to use for all groups for nuclide-reaction pairs for which cross-section-covariance data are too large or not available on input covariance data library. |
udcov_corr= |
1.0 |
User-defined default correlation value to use for nuclide-reaction pairs for which cross-section-covariance data are not available on the input covariance library. |
udcov_corr_type= |
zone |
User-defined default
correlation to use
for nuclide-reaction
pairs for which
cross-section-covariance
data are not
available on the
input covariance
library. Allowed
values are |
udcov_therm= |
0.0 |
User-defined default
value of standard
deviation in
cross-section data to
use for thermal data
for nuclide-reaction
pairs for which
cross-section-covariance
data are too large or
not available on
input covariance data
library. If input,
the |
udcov_inter= |
0.0 |
User-defined default
value of standard
deviation in
cross-section data to
use for intermediate
data for
nuclide-reaction
pairs for which
cross-section-covariance
data are too large or
not available on
input covariance data
library. If input,
the |
udcov_fast= |
0.0 |
User-defined default
value of standard
deviation in
cross-section data to
use for fast data for
nuclide-reaction
pairs for which
cross-section-covariance
data are too large or
not available on
input covariance data
library. If input,
the |
6.1.4.4.4. HTML and user-input covariance data
User-defined covariance data can be specified for individual nuclides
and reactions using the COVARIANCE data block. This data begins with
the keywords READ COVARIANCE and ends with the keywords
END COVARIANCE. Any of the optional COVARIANCE input data may be entered
in free form format between the READ COVARIANCE and END COVARIANCE
keywords. The specifications for the COVARIANCE data block are
described in User Input Covariance Data of the TSUNAMI Utility Modules
chapter.
As the SAMS module generates HTML output, the optional HTML data block
will provides user control over some formats of the output. This data
begins with the keywords READ HTML and ends with the keywords
END HTML. Any of the optional HTML input data may be entered in free form
format between the READ HTML and END HTML keywords. The
specifications for the HTML data block are described in
the TSUNAMI Utility Modules manual.
6.1.4.5. Input termination
The input specification for all TSUNAMI-1D sequences must terminate with
a line containing END in column 1. This END terminates the control
sequence.
6.1.5. Example Problems
Nine TSUNAMI-1D sample problems are included in the SCALE package to
verify successful installation and to provide examples for users. They
are provided in the smplprbs directory of the software distribution.
Three example problems are presented in this section and comparisons
among the different methods for cross-section processing are discussed.
The first problem presented is a variant of the TSUNAMI-1D1 keff
sensitivity sample problem with some addition input parameters in the
READ SAMS data block and using INFHOMMEDIUM unit cell type. The second
example problem presented in this section generates keff
sensitivities using the MULTIREGION unit cell type. The third example
problem is similar to the TSUNAMI-1D5 sample problem that demonstrates
the GPT capabilities. The five sample problems in the software package
are designed to run quickly and test most code features. The three
examples presented here are designed to produce accurate results, but
may require more computational resources.
For all problems the validity of the sensitivity coefficients should be confirmed through the use of direct perturbation sensitivity calculations. For each sensitivity coefficient examined by direct perturbation, the keff of the system is computed first with the nominal values of the input quantities, then with a selected input value increased by a certain percentage, and then with the value decreased by the same percentage. The direct perturbation sensitivity coefficient of keff to some input value \(\alpha\) is computed as
where\(\alpha^{+}\) and \(\alpha^{-}\) represent the increased and decreased values, respectively, of the input quantity \(\alpha\) and \(k_{\alpha^{+}}\) and \(k_{\alpha^{-}}\) represent the corresponding values of keff.
The use of direct perturbation calculations to confirm the validity of sensitivity coefficients is strongly encouraged. Inconsistent modeling between the resonance-self shielding input and the criticality problem description can lead to erroneous sensitivity results. These erroneous results can be revealed through the use of direct perturbation confirmation of the energy-integrated sensitivity results for the total cross section. The total cross-section sensitivities are equivalent to number density sensitivities on an energy-integrated basis.
The results shown here were generated with a previous version of SCALE, so current data libraries and code implementations may product different results. However, the techniques demonstrated are applicable to the current version of TSUNAMI-1D.
6.1.5.1. INFHOMMEDIUM sample problem
The selected sample problem with INFHOMMEDIUM cross-section processing is based on an unreflected rectangular parallelepiped consisting of a homogeneous mixture of UF4 and paraffin with an enrichment of 2% in 235U. The H/235U atomic ratio is 294:1. The dimensions of the experiment were 56.22 cm \(\times\) 56.22 cm \(\times\) 122.47 cm. [TS-1D-CLP86]. For the purposes of this exercise, this experiment was modeled as a sphere with a critical radius of 38.50 cm. This model is consistent with SCALE sample problem TSUNAMI-1D1, which utilizes the 238-group ENDF/B-VII cross-section library, and the default cross-section processing with BONAMIST and CENTRM/PMC/WORKER.
An annotated TSUNAMI-1D1 input for this experiment is shown in
Sect. 6.1.3.1. The composition data is input as number densities for each
nuclide. Because the material is treated as INFHOMMEDIUM, no explicit
unit cell model is necessary, and the READ CELL block is omitted. The
criticality description contains optional parameter data to change the
default S16 angular quadrature set to S8. The change
in angular quadrature is made only to demonstrate the input capabilities
of TSUNAMI-1D and has little effect on this calculation. The criticality
problem geometry uses a spherical coordinate system with the default
boundary conditions (reflected left, vacuum right). The system consists
of a single material zone containing mixture 1 with a radius of
38.50 cm. The optional sensitivity calculation data block was entered to
request the extended edit of sensitivity by material zone (prtgeom),
the extended edits of the explicit, implicit and complete sensitivity
coefficients (prtimp), and corrections in the cross-section covariance
data (use_dcov, cov_fix).
Prior to producing the output of the functional modules, TSUNAMI-1D produces output from the XSProc routines as it is processing the user input and creating internal inputs for the resonance processing codes. TSUNAMI-1D also prints information regarding the criticality description.

Fig. 6.1.2 TSUNAMI-1D INFHOMMEDIUM sample problem input.
For this problem, direct perturbation results were obtained for the
number densities of each nuclide. In these calculations, the number
density of each nuclide was perturbed by \(\pm2\%\) and the calculation was
repeated using the TSUNAMI-1DC sequence. The sensitivity of keff to
the number density is equivalent to the sensitivity of keff to the
total cross section, integrated over energy. The direct perturbation
sensitivity coefficients were computed by using the keff values from
the unperturbed and perturbed cases in Eq. (6.1.15). To demonstrate the
importance of the sensitivity to the resonance processing implicit
sensitivity computed by BONAMIST, the same model shown in Fig. 6.1.2
was run with TSUNAMI-1D with PARM=CENTRM. The results from the
INFHOMMEDIUM sample problem are given in Table 6.1.8. The TSUNAMI-1D
results using the default codes for resonance processing show good
agreement with the direct perturbation results for all nuclides. Due to
omission of the implicit terms, the TSUNAMI-1D results with PARM=CENTRM
do not show good agreement with the direct perturbation for this thermal
system. The maximum difference between the direct perturbation results
and the TSUNAMI-1D results occurs for 238U with a magnitude of
1.5%. The maximum difference between the direct perturbation results and
the TSUNAMI-1D with PARM=CENTRM results occurs for 238U with a
magnitude of 19%. Thus, the use of the default PARM=BONAMIST is
recommended.
Isotope |
Reaction |
Direct perturbation |
TSUNAMI-1D |
TSUNAMI-1D PARM=CENTRM** |
|---|---|---|---|---|
1H |
total |
2.20E-01 |
2.18E-01 |
2.52E-01 |
1H |
scatter |
3.19E-01 |
3.53E-01 |
|
1H |
elastic |
3.19E-01 |
3.53E-01 |
|
1H |
capture |
-1.01E-01 |
-1.01E-01 |
|
1H |
n, \(gamma\) |
-1.01E-01 |
-1.01E-01 |
|
12C |
total |
2.41E-02 |
2.38E-02 |
2.76E-02 |
12C |
scatter |
2.45E-02 |
2.83E-02 |
|
12C |
elastic |
2.43E-02 |
2.80E-02 |
|
12C |
n,n’ |
2.20E-04 |
2.20E-04 |
|
12C |
capture |
-6.83E-04 |
-6.83E-04 |
|
12C |
n, \(gamma\) |
-4.98E-04 |
-4.98E-04 |
|
12C |
n,p |
-3.53E-08 |
-3.53E-08 |
|
12C |
n,d |
-7.33E-08 |
-7.33E-08 |
|
12C |
n, \(alpha\) |
-1.85E-04 |
-1.85E-04 |
|
19F |
total |
4.10E-02 |
4.06E-02 |
4.47E-02 |
19F |
scatter |
4.62E-02 |
5.03E-02 |
|
19F |
elastic |
2.94E-02 |
3.34E-02 |
|
19F |
n,n’ |
1.58E-02 |
1.58E-02 |
|
19F |
n,2n |
2.89E-06 |
2.89E-06 |
|
19F |
capture |
-5.59E-03 |
-5.59E-03 |
|
19F |
n, \(gamma\) |
-2.39E-03 |
-2.39E-03 |
|
19F |
n,p |
-2.37E-04 |
-2.37E-04 |
|
19F |
n,d |
-1.27E-05 |
-1.27E-05 |
|
19F |
n,t |
-2.72E-06 |
-2.72E-06 |
|
19F |
n, \(alpha\) |
-2.96E-03 |
-2.96E-03 |
|
235U |
total |
2.52E-01 |
2.52E-01 |
2.53E-01 |
235U |
scatter |
4.32E-04 |
5.03E-04 |
|
235U |
elastic |
2.02E-04 |
2.73E-04 |
|
235U |
n,n’ |
2.13E-04 |
2.13E-04 |
|
235U |
n,2n |
1.70E-05 |
1.70E-05 |
|
235U |
fission |
3.64E-01 |
3.65E-01 |
|
235U |
capture |
-1.13E-01 |
-1.12E-01 |
|
235U |
n, \(gamma\) |
-1.13E-01 |
-1.12E-01 |
|
235U |
nubar |
9.50E-01 |
9.50E-01 |
|
235U |
\(\chi\) |
8.52E-08 |
8.52E-08 |
|
238U |
total |
-2.08E-01 |
-2.05E-01 |
-2.47E-01 |
238U |
scatter |
4.81E-02 |
2.46E-02 |
|
238U |
elastic |
3.46E-02 |
1.10E-02 |
|
238U |
n,n’ |
1.25E-02 |
1.25E-02 |
|
238U |
n,2n |
1.02E-03 |
1.02E-03 |
|
238U |
fission |
3.35E-02 |
3.35E-02 |
|
238U |
capture |
-2.86E-01 |
-3.05E-01 |
|
238U |
n, \(gamma\) |
-2.86E-01 |
-3.05E-01 |
|
238U |
nubar |
5.02E-02 |
5.02E-02 |
|
238U |
\(\chi\) |
4.54E-09 |
4.54E-09 |
The uncertainty information from SAMS for the INFHOMMEDIUM sample problem is shown in Example 6.1.1. Based on the 44GROUPCOV covariance data library, documented in the COVLIB chapter, the uncertainty in keff due to these covariance data is 0.6064% \(\Delta k/k\). A more detailed description of the uncertainty information is given in Chapter 6.3. Some plots of the energy-dependent sensitivity data were generated with Fulcrum. The energy-dependent data is available in the sensitivity data file, which is returned to the same directory as the input file and given the same name as the user’s input file with the extension .sdf. Energy-dependent sensitivity profiles for 235U fission and 1H elastic scattering are shown in Fig. 6.1.3. The 238U capture sensitivity profiles from TSUNAMI-1D and TSUNAMI-1D with PARM=CENTRM are shown in Fig. 6.1.4. The effect of the implicit component of the sensitivity coefficients can be seen in the resonance region in the difference between the TSUNAMI-1D and TSUNAMI-1D PARM=CENTRM profiles.
-----------------------------
Uncertainty Information
-----------------------------
the relative standard deviation of k-eff (% delta-k/k) due
to cross-section covariance data is:
0.6064 % delta-k/k
contributions to uncertainty in k-eff (% delta-k/k) by
individual energy covariance matrices:
covariance matrix
nuclide-reaction with nuclide-reaction % delta-k/k due to this matrix
------------------------------ ------------------------------- ----------------------------------
u-238 n,gamma u-238 n,gamma 3.8595E-01
u-235 nubar u-235 nubar 2.8506E-01
u-238 n,n' u-238 n,n' 2.1331E-01
u-235 n,gamma u-235 n,gamma 1.5963E-01
f-19 elastic f-19 elastic 1.3392E-01
u-238 elastic u-238 n,n' -1.2469E-01
u-235 fission u-235 n,gamma 1.2396E-01
u-235 fission u-235 fission 1.2185E-01
h-1 elastic h-1 elastic 1.1625E-01
f-19 elastic f-19 n,n' -1.1598E-01
f-19 n,n' f-19 n,n' 1.1072E-01
u-235 chi u-235 chi 8.4524E-02
u-238 elastic u-238 elastic 6.8573E-02
u-238 nubar u-238 nubar 5.8699E-02
h-1 n,gamma h-1 n,gamma 5.0686E-02
u-238 elastic u-238 n,gamma 4.9596E-02
f-19 n,alpha f-19 n,alpha 1.9853E-02
u-238 fission u-238 fission 1.7402E-02
c elastic c elastic 1.5259E-02
u-238 n,2n u-238 n,2n 1.3655E-02
f-19 n,gamma f-19 n,gamma 9.7725E-03
c n,n' c elastic -8.8958E-03
c n,n' c n,n' 8.4710E-03
f-19 elastic f-19 n,alpha 6.6444E-03
u-238 chi u-238 chi 5.6329E-03
u-235 elastic u-235 n,gamma 4.4651E-03
u-235 elastic u-235 fission -3.2889E-03
u-238 fission u-238 n,gamma 2.7666E-03
f-19 n,p f-19 n,p 2.0768E-03
u-238 elastic u-238 n,2n -1.8932E-03
u-238 elastic u-238 fission -1.8189E-03
c n,alpha c n,alpha 1.6172E-03
c n,gamma c n,gamma 1.4880E-03
u-235 n,n' u-235 n,n' 1.3414E-03
u-235 elastic u-235 n,n' -8.6275E-04
f-19 elastic f-19 n,p 5.8397E-04
f-19 elastic f-19 n,gamma 4.5179E-04
u-235 elastic u-235 elastic 4.3646E-04
f-19 n,d f-19 n,d 2.8169E-04
u-235 n,2n u-235 n,2n 1.5476E-04
c n,n' c n,alpha -1.4865E-04
f-19 elastic f-19 n,2n -7.0280E-05
f-19 elastic f-19 n,d 6.6324E-05
f-19 n,t f-19 n,t 6.5613E-05
u-235 elastic u-235 n,2n -2.7763E-05
f-19 n,2n f-19 n,2n 2.2764E-05
f-19 n,n' f-19 n,2n -1.9276E-05
f-19 elastic f-19 n,t 1.4593E-05
c n,n' c n,gamma 6.9724E-06
c n,d c n,d 8.5422E-07
c n,p c n,p 4.5780E-07
c n,n' c n,d -3.2157E-07
c n,n' c n,p -1.5591E-07
Note: relative standard deviation in k-eff can be computed from individual values by adding the square of the values with positive signs and subtracting the square of the values with negative signs, then taking the square root
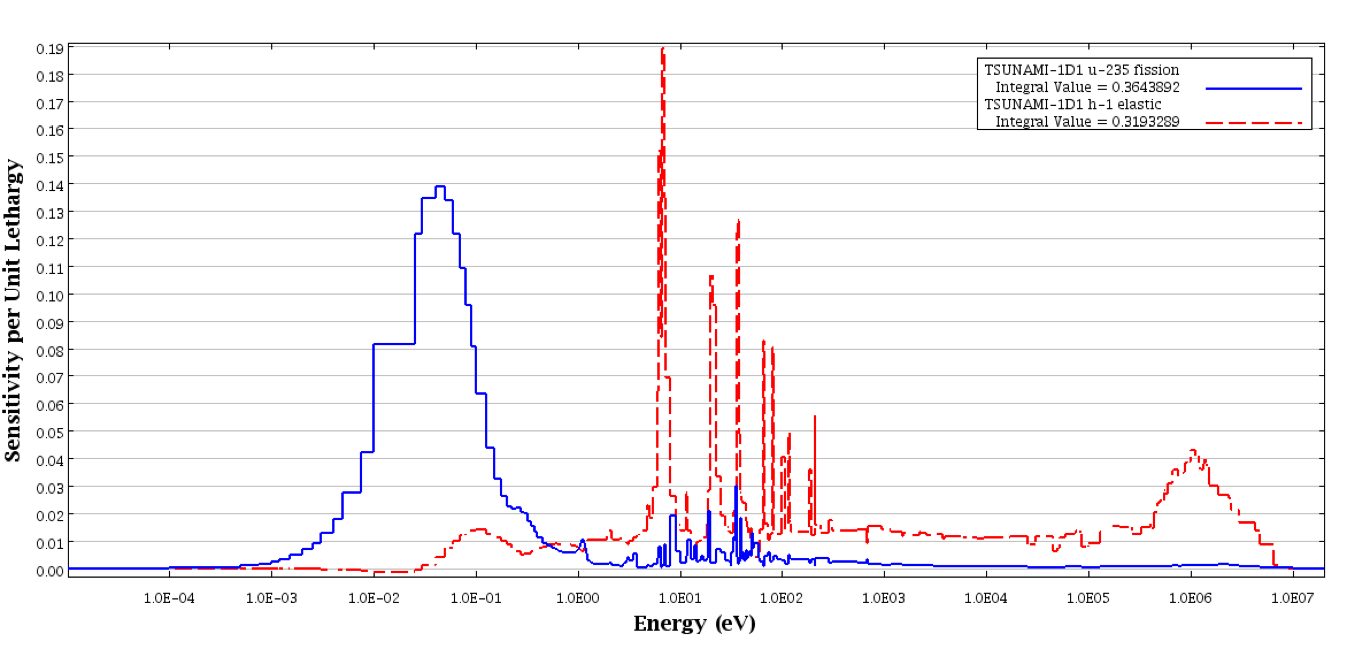
Fig. 6.1.3 Energy-dependent sensitivity profiles from TSUNAMI-1D for INFHOMMEDIUM sample problem.
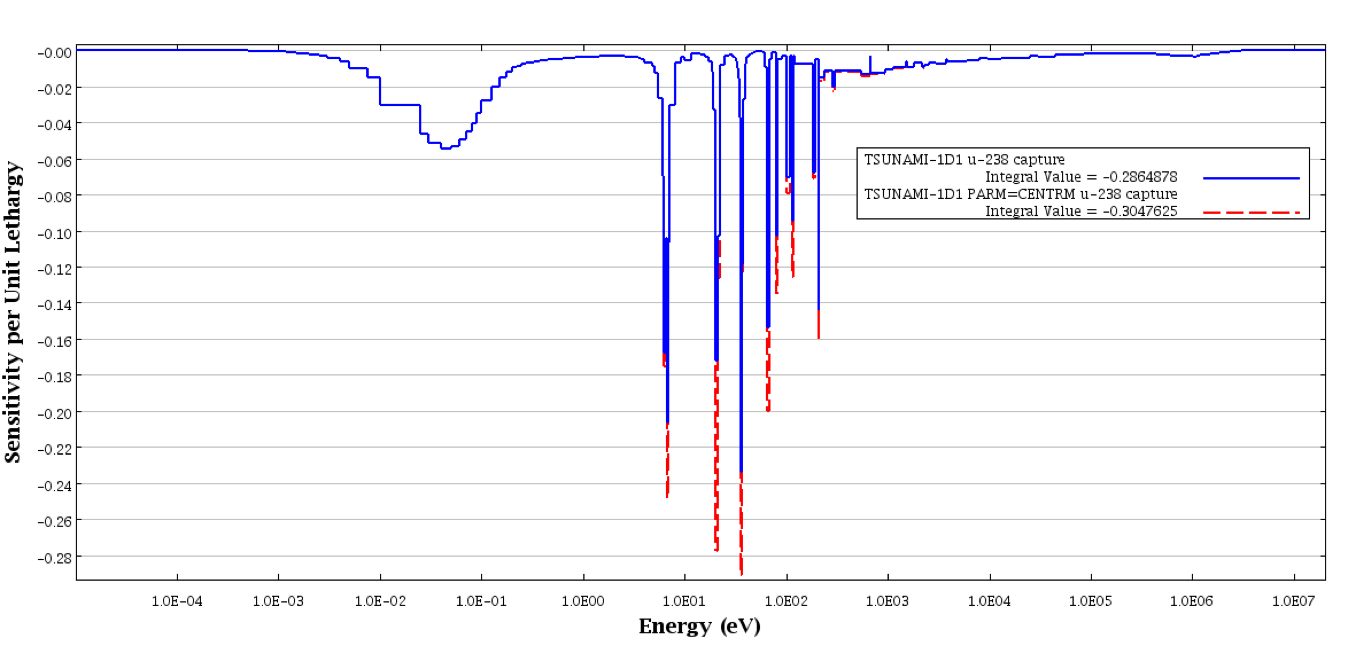
Fig. 6.1.4 Comparison of 238U capture sensitivities from TSUNAMI-1D and TSUNAMI-1D with PARM=CENTRM for INFHOMMEDIUM sample problem.
6.1.5.2. Multiregion sample problem
The sample problem selected to demonstrate the use of TSUNAMI-1D with
MULTIREGION cross-section processing is the FLATTOP-25 metal system from
the Cross-Section Evaluation Working Group benchmark
specifications. [TS-1D-AKPZ74]. The system consists of a 6.116-cm sphere of
93%-enriched uranium with a natural uranium reflector. The outer radius
of the reflector is 24.13 cm. The system is used for sample problems
TSUNAMI-1D4 – TSUNAMI-1D7. For this example, input for TSUNAMI-1D4 was
modified to use the SCALE 238-group ENDF/B-VII library with multiregion
cell data as shown in Fig. 6.1.5. The multiregion cell data processes
the cross sections in the same geometry as the criticality model.
Therefore, the dimensions of the system are input twice in this model:
once in the unit cell specification portion of the input and once in the
criticality portion of the input. The unit cell specification geometry
is used to generate input for BONAMIST and CENTRM/PMC/WORKER, and the
criticality model is used to generate input for the forward and adjoint
XSDRNPM calculations. The optional sensitivity calculation data block
was entered to request the extended edit of sensitivity by material zone
(prtgeom), the extended edits of the explicit, implicit and complete
sensitivity coefficients (prtimp), and to allow larger implicit
sensitivity values to be computed without producing warning messages
(largeimp=1000).
This model was executed with TSUNAMI-1D and also with TSUNAMI-1D with PARM=CENTRM. Direct perturbation sensitivity results were obtained for the number densities of all nuclides, which correspond to the sensitivity of keff to the total cross section, integrated over energy. The energy-integrated sensitivity results are shown in Table 6.1.9. The TSUNAMI-1D results agree well with the direct perturbation results for this system. The maximum difference occurs for 238U in the reflector region with a magnitude of 0.9%. Because this is a fast system, the effect of the resonance processing on the sensitivity coefficients is minimal. Thus, the TSUNAMI-1D PARM=CENTRM results are almost identical to the default TSUNAMI-1D results with BONAMIST.
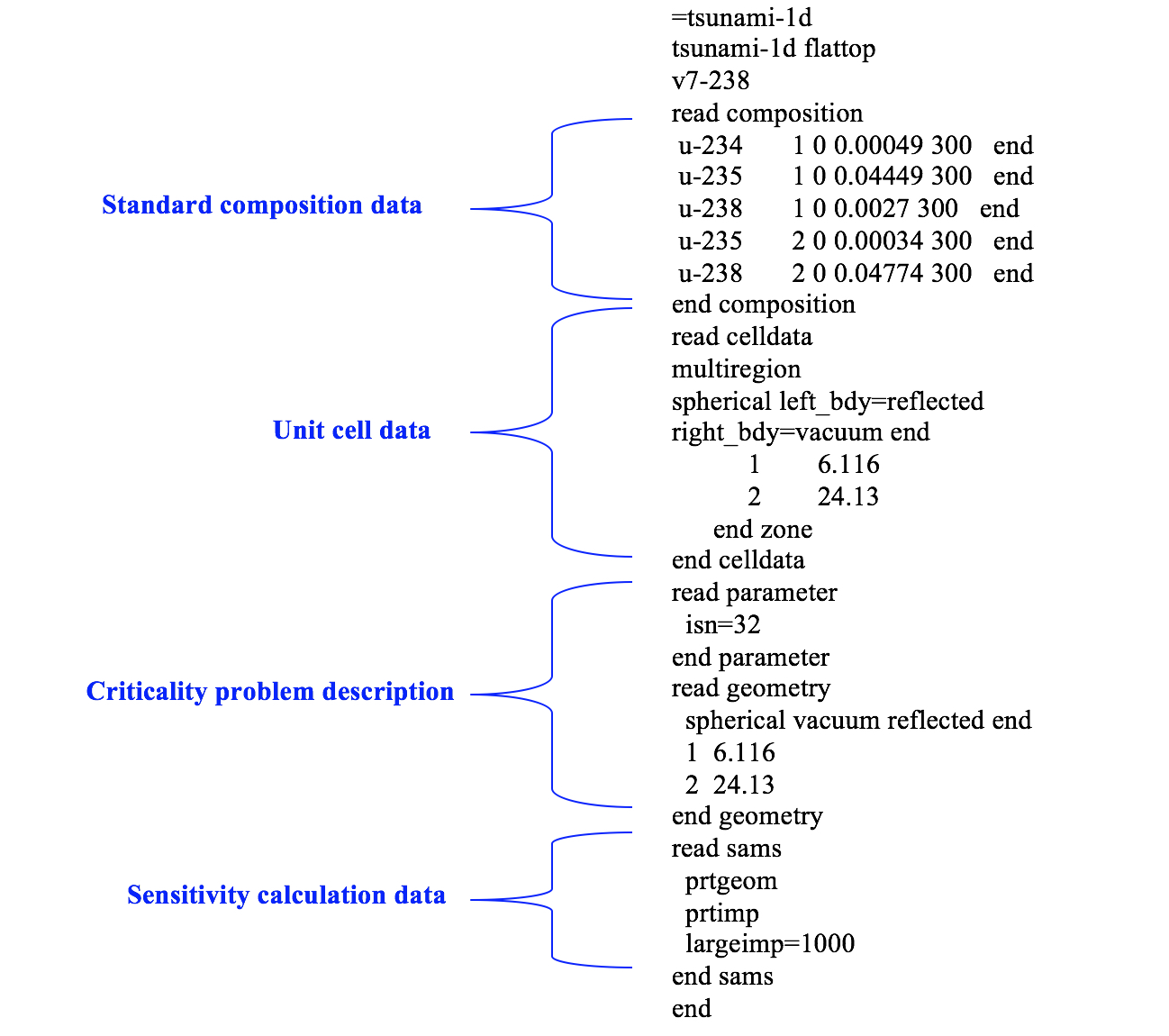
Fig. 6.1.5 TSUNAMI-1D MULTIREGION sample problem input.
The uncertainty information from SAMS HTML output for the multiregion sample problem is shown in Fig. 6.1.6. Based on the 44GROUPCOV covariance data file, the uncertainty in keff due to these covariance data is 1.2743% \(\Delta k/k\). The contributions to this uncertainty are listed by nuclide. These data are explained in more detail in the SAMS chapter.
Sensitivity profiles from TSUNAMI-1D for 235U fission in zone 1 (core) and zone 2 (reflector) were generated with Fulcrum and are shown in Fig. 6.1.7. Additionally, sensitivity profiles for 238U capture in zone 1 and zone 2 are shown in Fig. 6.1.8. Note that the capture sensitivities are negative, such that the lower curve has the greater magnitude. In 235U and 238U sensitivity profiles, the effect of the differing enrichments in the core and the reflector of this system are demonstrated with the much greater sensitivity to 235U fission in the core and to 238U capture in the reflector.
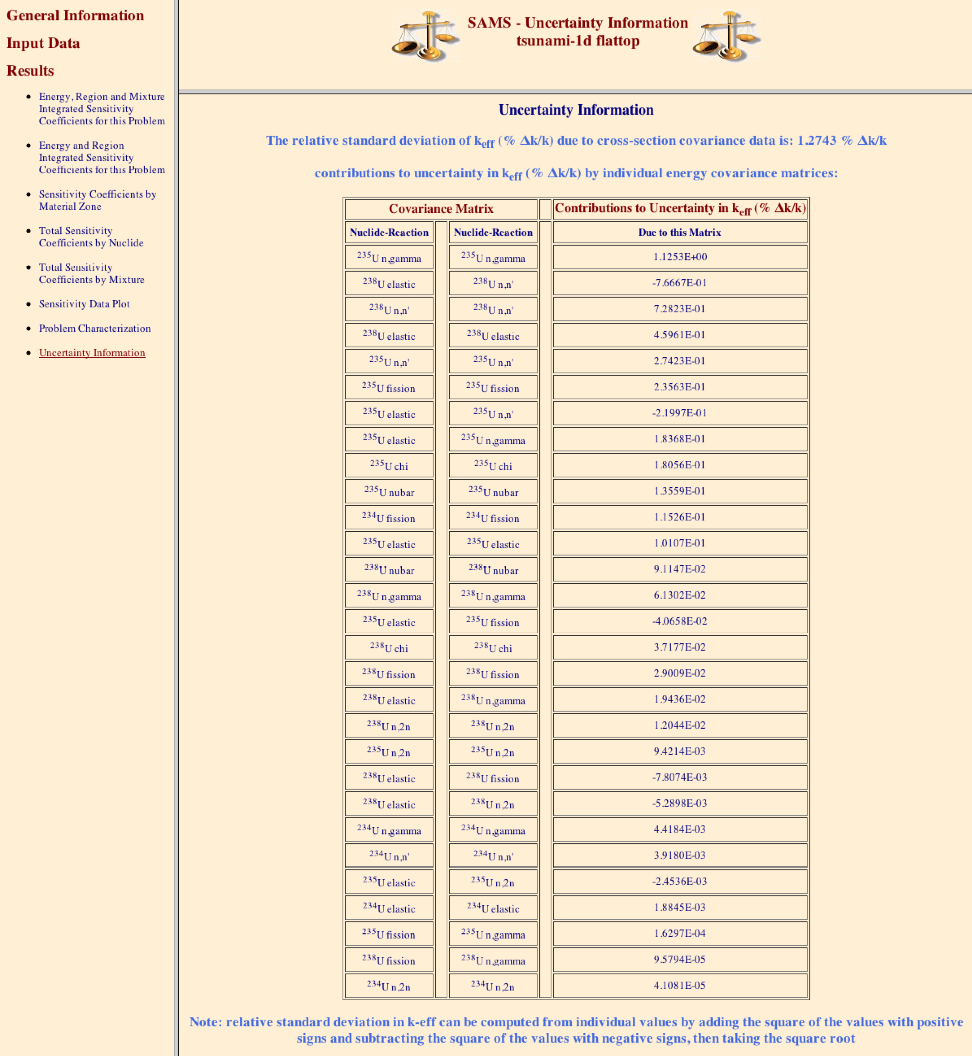
Fig. 6.1.6 Uncertainty information in HTML output from MULTIREGION sample problem.
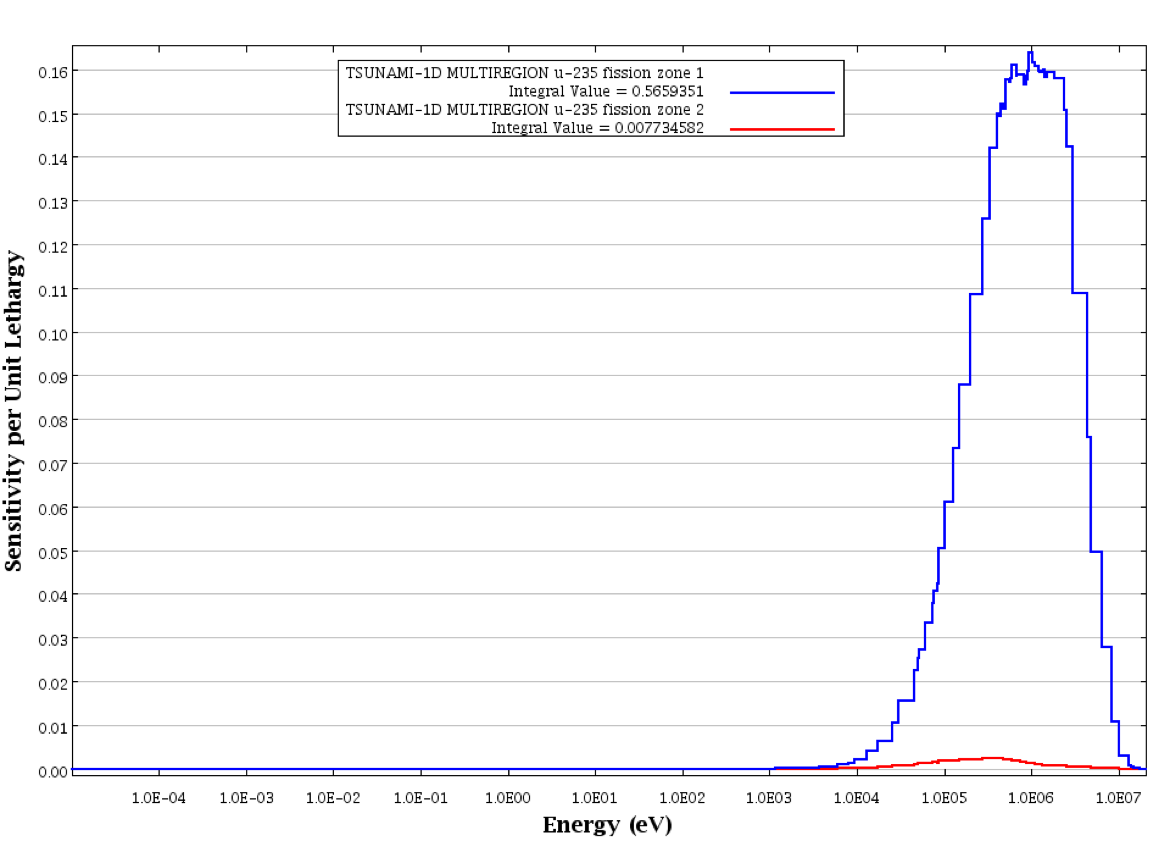
Fig. 6.1.7 Sensitivity profiles from TSUNAMI-1D for 235U fission in zone 1 and zone 2 of MULTIREGION sample problem.
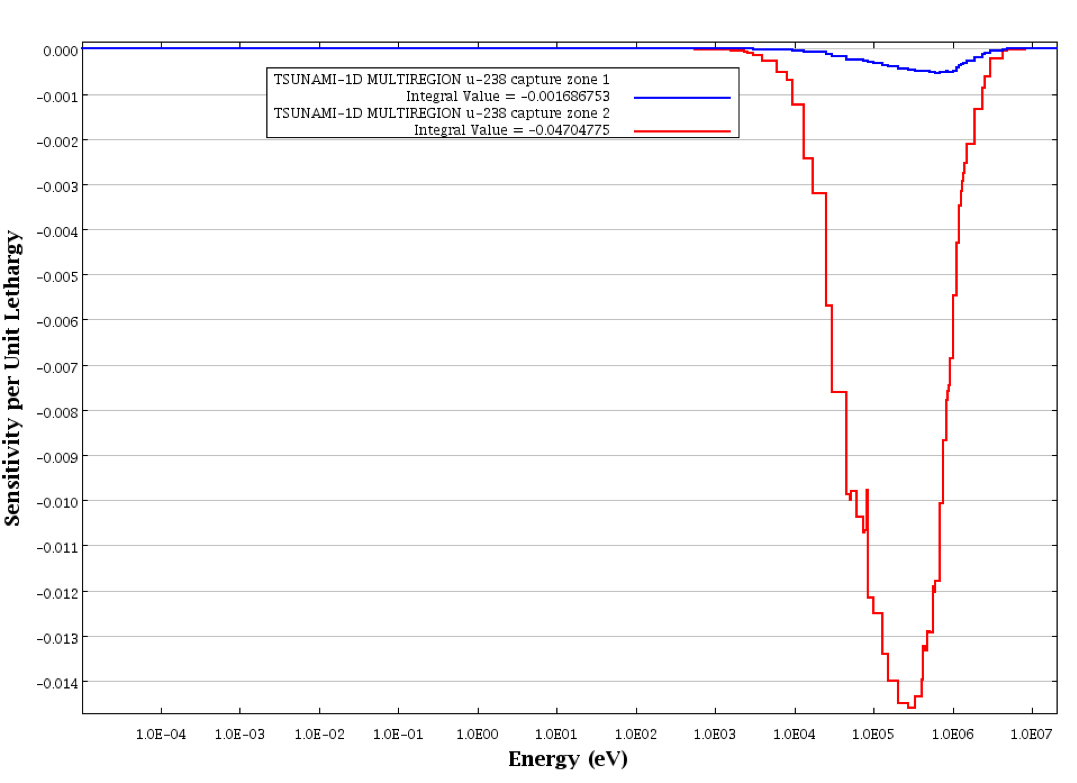
Fig. 6.1.8 Sensitivity profiles from TSUNAMI-1D for 238U capture in zone 1 and zone 2 of MULTIREGION sample problem.
6.1.5.3. GPT sample problem
The sample problem selected to demonstrate the use of TSUNAMI-1D with
Generalized Perturbation theory is from the OECD LWR Uncertainty
Analysis in Modeling benchmark specification [TS-1D-IAKS07].
The system consists of a 4.85% enriched uranium PWR fuel pin modeled at 551 K. This
system is used for sample problem TSUNAMI-1D9. For this example, the
DEFINITIONS and SYSTEMRESPONSES blocks are used to define six
additional response ratios for sensitivity and uncertainty analysis. The
requested responses in the benchmark were for the energy-integrated
fission and absorption microscopic cross-sections for 234U,
235U, and 238U. The input for this sample problem is
provided in Example 6.1.2. For this sample, seven separate sensitivity
data files are generated, one for each of the six defined responses in
addition to keff. Selected sensitivity profiles are shown in
Fig. 6.1.9 for the 238U (n,\(\gamma\)) cross-section. This figure
shows the negative sensitivity of keff due to 238U
resonance absorption in the blue profile. The red profile shows the
positive sensitivity of the energy-integrated 238U absorption
cross-section due to the multigroup 238U (n,\(\gamma\)) cross-section.
The large positive magnitude of this sensitivity is predominantly due to
the presence of the 238U (n,\(\gamma\)) cross-section directly in the
definition of the response ratio. In contrast, the black sensitivity
profile shows the negative sensitivity of the energy-integrated
235U fission cross-section due to the multigroup 238U
(n,\(\gamma\)) cross-section. In this response, positive perturbations to the
238U (n,\(\gamma\)) multigroup cross-sections induce changes in the
flux spectra that lead to a decrease in the energy-integrated
235U fission cross-section. These indirect sensitivity effects
are determined by the solution of the generalized adjoint calculations.
=tsunami-1d
PWR Unit Cell
v7-238
read comp
'fuel
uo2 10 den=10.283 1 551.0 92235 4.85 92234 0.045 92238 95.105 end
zirc4 20 1 551.0 end
h2o 30 den=0.766 1 551.0 end
he 40 den=0.00125 1 551.0 end
end comp
read celldata
latticecell squarepitch pitch=1.4427 30 fueld=0.9391 10 cladd=1.0928 20 gapd=0.9582 40 end
end celldata
read geom
cylindrical white reflected end
10 .46955 40 .4791 20 .5464 30 .813956
end geom
read definitions
response 1 nuclide=92234 mt=102 mixture=10 micro end response
response 2 nuclide=92234 mt= 18 mixture=10 micro end response
response 3 nuclide=92235 mt=102 mixture=10 micro end response
response 4 nuclide=92235 mt= 18 mixture=10 micro end response
response 5 nuclide=92238 mt=102 mixture=10 micro end response
response 6 nuclide=92238 mt= 18 mixture=10 micro end response
response 7 unity multimix 10 20 30 40 end end response
end definitions
read systemresponses
ratio 1 numer 1 2 end denom 7 end title='U234-abs' end ratio
ratio 2 numer 2 end denom 7 end title='U234-fis' end ratio
ratio 3 numer 3 4 end denom 7 end title='U235-abs' end ratio
ratio 4 numer 4 end denom 7 end title='U235-fis' end ratio
ratio 5 numer 5 6 end denom 7 end title='U238-abs' end ratio
ratio 6 numer 6 end denom 7 end title='U238-fis' end ratio
end systemresponses
end
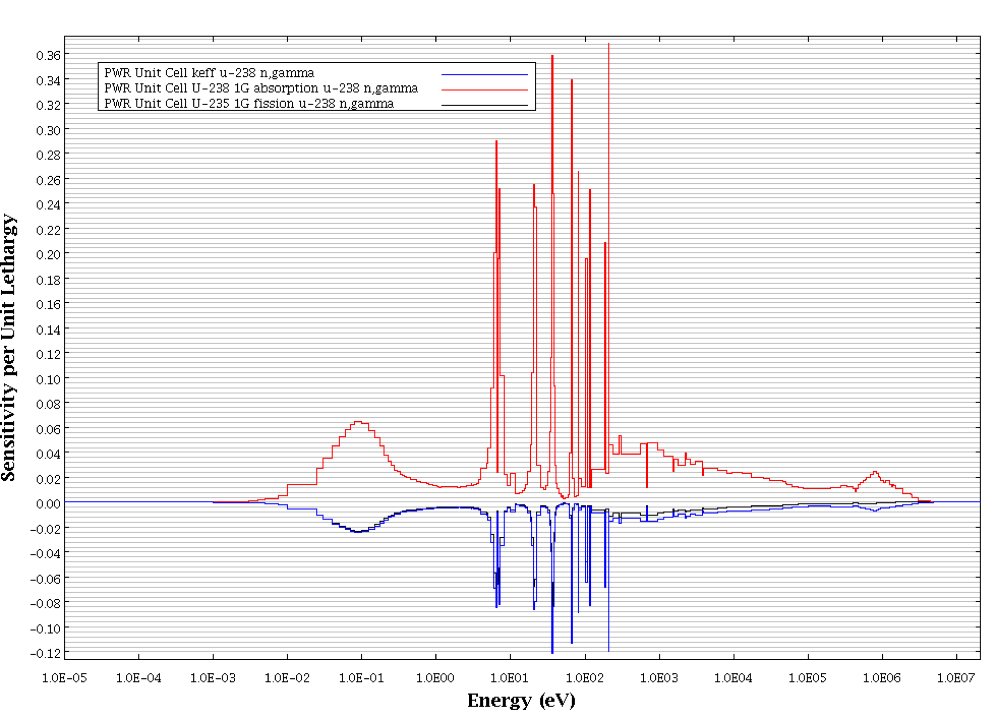
Fig. 6.1.9 Response Sensitivities to 238U n,gamma cross section for the TSUNAMI-1D9 sample problem.
References
- TS-1D-AKPZ74
H. Alter, R. Kidman, R. B. abd Labauv, R. Protsik, and B. A. Zolotar. Cross Section Evaluation Working Group Benchmark Specification. Technical Report BNL 19302, National Neutron Cross Section Center (ENDF-202), Brookhaven National Laboratory , Upton, NY (USA), 11 1974.
- TS-1D-CLP86
Wilfred C., N. F. Landers, and L. M. Petrie. Validation of KENO V.a Comparison with Critical Experiments. Technical Report ORNL/CSD/TM-238, Oak Ridge National Laboratory, Oak Ridge, TN (USA), 12 1986.
- TS-1D-IAKS07
Kalcko Ivanov, M. Avramova, Ivan Aleksander Kodeli, and E. Sartori. Benchmark for uncertainty analysis in modeling (UAM) for design, operation and safety analysis of LWRs. Citeseer, 2007.